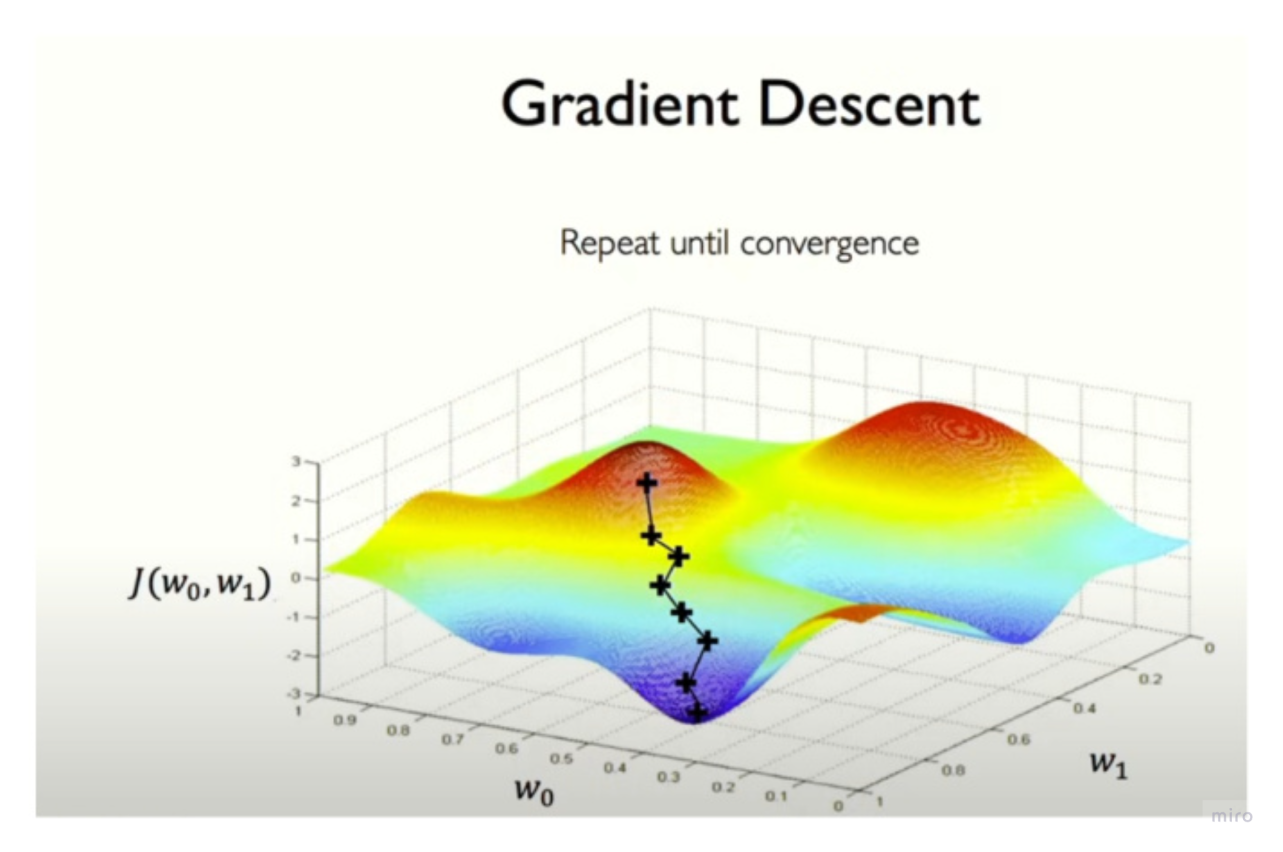
Gradient descent is an iterative algorithm for minimizing a loss function by moving the model parameters in the direction that most rapidly decreases the loss.
Process:
- Start initially with random weights for all inputs. Compute the loss.
- Calculate the gradient of loss with respect to that initial setting of weights.
- In one-dimension, gradient is basically the derivative
- In multi-dimension, gradient is itself a vector
- The gradient at any point always points in the direction of steepest local increase of that loss. The gradient only tells us about the local slope; “uphill” from where we are might still eventually lead us into a different valley, etc. But locally, it always points toward increase (away from the minimum)
- Change (update) the weights a small amount in the opposite direction of the gradient
- How large or small step change should we do in a given direction? That’s called the learning rate.
- Too small a step → learning is very slow.
- Too large → updates can “overshoot” the minimum and make training unstable or diverge.
Stochastic Gradient Descent
- In full-batch gradient descent, each update uses all data points to compute the gradient. This is expensive for large datasets because every update requires a full pass over the data.
- Stochastic Gradient Descent (SGD) instead uses a single randomly sampled data point to estimate the gradient and update the weights. Each update is much cheaper, but noisier.
- In practice we almost always use mini-batch SGD (e.g. 32, 64, 256) to estimate the gradient. This reduces noise compared to pure single-example SGD, can parallelize computation and achieve high speeds on GPUs.
- According to Anil Ananthaswamy (Page 85), since the error (loss) calculated for a certain sample of data doesn’t fully represent all possible errors, the gradient towards minimum is only an approximation. Sometimes it’s pointing in the right direction, but most times it’s not. In SGD, the word “stochastic” refers to the fact that the direction of each step in the descent is slightly random.
Primary Resources
- Why Machines Learn, Chapter 3 (Bottom of the bowl) page 68-71. It takes the simple example of going down the slope for a 2D curve given by a convex y=x2 function. Derivative (from calculus) is the way of finding the slope at any point along the curve. That slope (derivative) is zero at the minimum of the function – bottom of the bowl-like curve.
