Layers

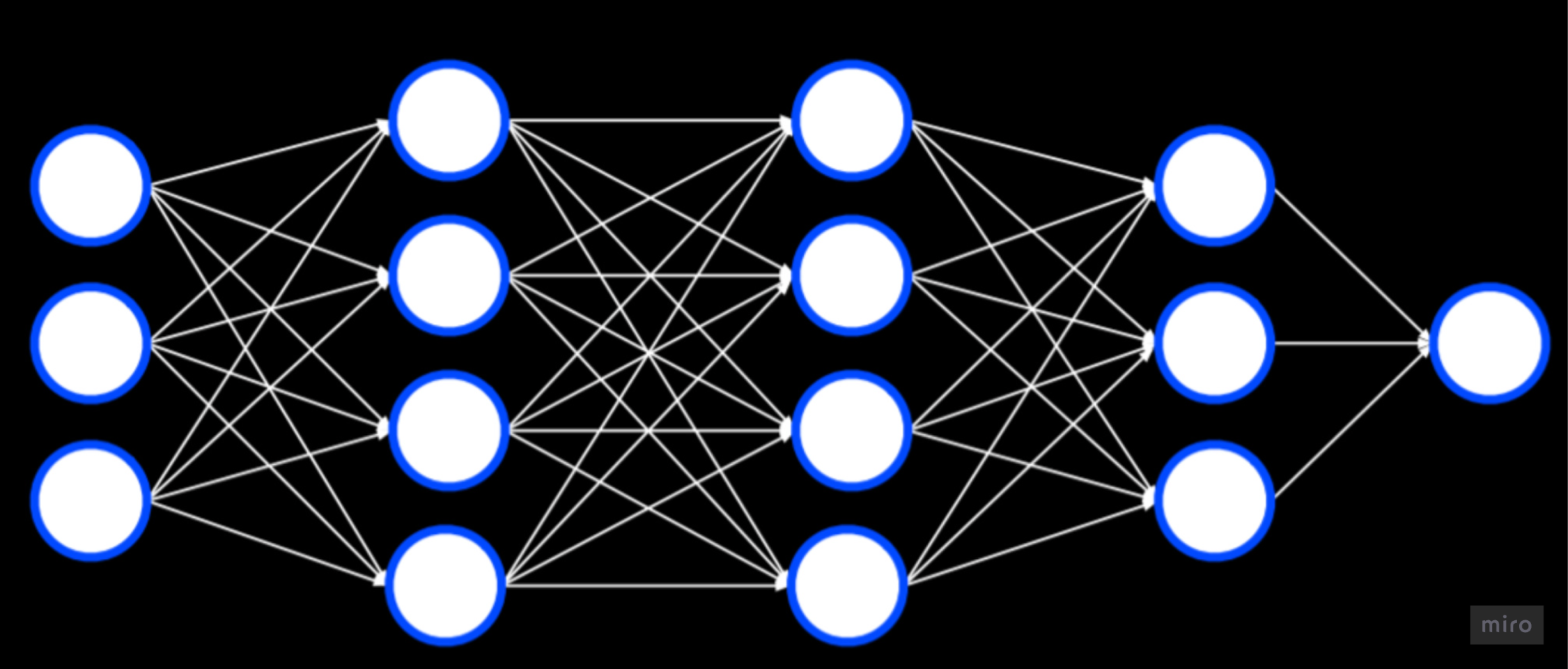
Layers = groups of perceptrons (See [[Perceptron]]) stacked so that each layer’s outputs become the next layer’s inputs, letting the network learn increasingly abstract features.

• Stacked/layered perceptrons create a feed-forward network (ie going from an input to an output layer, never backwards).
• The layers between input and output are called hidden layers because they are the intermediate transformations we don’t directly observe in the input data.

Intuition

• When you put many perceptrons in a layer, each neuron learns a different linear boundary or feature (i.e. calculates something different about the input dataset)
• When you stack multiple layers, each layer is operating on the transformed outputs of the previous (combined learning is being passed to the next layer)
• This is why deep networks learn hierarchical abstractions. Early layers tend to capture local/low-level patterns and later layers tend to capture more global/high-level patterns.
• Multiple layers → Multi-Layered Perceptron (MLP) → hence "Deep" Learning.
• Deep neural networks are the ‘astonishing descendants of perceptrons’ – Anil Anathaswamy (Page 25)

Complex stuff

• Some activation functions are threshold functions (or Step Activation Functions). Eg. ReLU One of the problems with thresholding function is that it doesn’t have a derivative (slope) everywhere. The slope is zero always, except at the point of transition, where it is infinite.
• But the Sigmoid activation function has a smooth, rather than abrupt, transition from 0 to 1. This smoothness is important for training networks with hidden layers.
• The basic idea is that each hidden neuron is generating some sigmoidal curve, where the steepness of the curve is controlled by neuron’s input weight and the location at which the curve rises along the x axis (i.e. goes from -x to +x) is controlled by the neuron’s bias.
• If we graph it, this effectively creates a rectangular output from each sigmoidal neuron: where the weights dictate the length and width (because steepness of the curve defines how tall and skinny the rectangle is) and the bias value dictates how much further right is the rectangle shifted (on x axis)
• So with multiple hidden sigmoidal neurons we can create multiple rectangles of different shapes (using bespoke weights) and stack them side by side (using bespoke biases)
• The linear combination of summing up all such biased and weighted outputs is what starts to approximate the actual desired function. As we increase the number of neurons, the power of this approach becomes obvious (imagine very thin rectangles densely packed side by side, under the original desired curve – they start to cover the entire area under the curve).
• In practice, a few hundred neurons are sufficient for astonishing results in most cases. A training algorithm like backpropagation is basically finding best set of weights and biases to approximate the original function.
• It has been mathematically proven that single-hidden-layer neural network, with enough neurons, can approximate any function. Universal Approximation theorem states: A neural network with just one hidden layer, a suitable non-linear activation, and enough neurons can approximate any continuous function on a bounded input region arbitrarily well. Another way to say it: If you only care about your function on some reasonable finite range of inputs, then by making a 1-hidden-layer network big enough, you can make its outputs as close as you like to the true function on that range. Chapter 9 of Why Machines Learn is all about this.
• CNN and RNN often have MLP-style layers after their special components.

Primary resources

• Amazing interactive tool by TensorFlow that lets you to see effect of depth/width/activations
• 3Blue1Brown’s video on Deep Learning, Chapter 1
• First 3 min of this 2016 CNN Explainer video from Computerphile explains that each node in a layer is a combination of previous layer’s nodes, creating a complicated function.. and with successive layers, it becomes combination of combinations. That’s what creates the abstraction (of features) aspect of deep learning. The rest of the video gets into CNNs.
• Why Machines Learn, Chapter 9, Pages 281-284. The perceptron training algorithm doesn’t work when the network has more than one weight matrix. Training a deep neural network is akin to finding the function that best approximates the relation between inputs and outputs. Then, given a new input, the function can be used to predict the output. In context of ChatGPT, the function represents its ability to learn an extremely complicated probability distribution that models the training data and then to sample from it – thus enabling the AI to generate new data that is in accordance with the statistics of the training data.
• Page 287-296 of Why Machines Learn book explains the buildup to Universal Approximation Theorem beautifully.